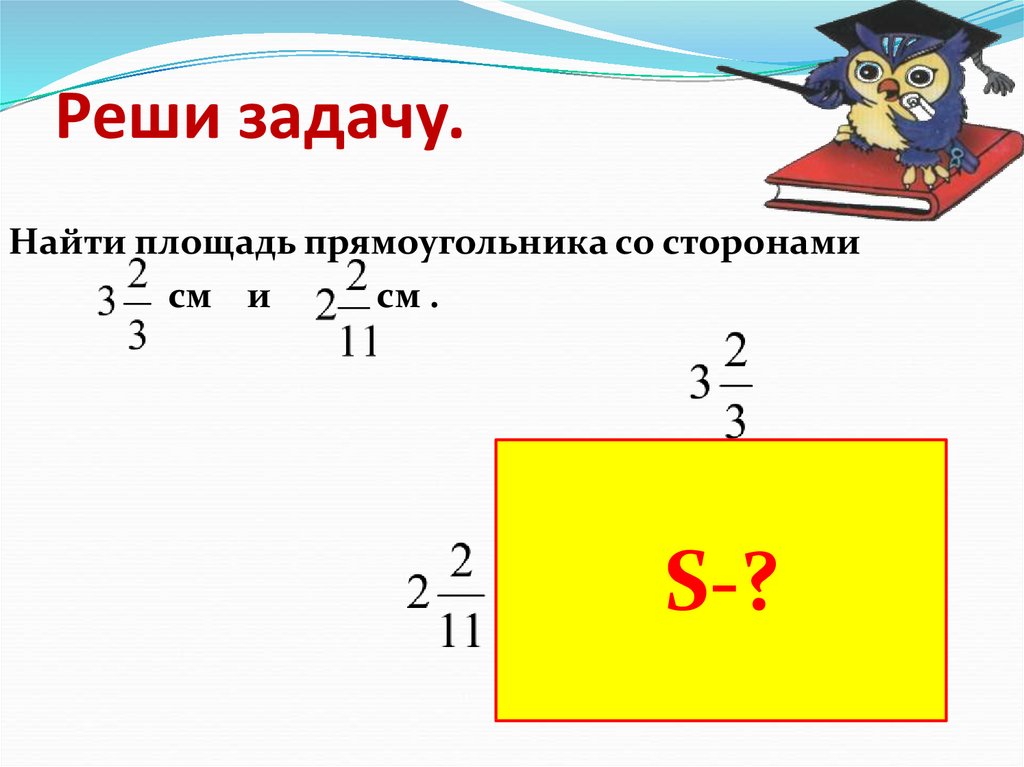
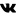Как решать площадь: Как найти площадь фигуры, формула

§ Площадь фигур. Площадь квадрата. Площадь прямоугольника. Площадь сложной фигуры

Определение площади Формулы площадей фигур

Две фигуры называют равными, если одну их них можно так наложить на другую, что эти фигуры совпадут.

Площади равных фигур равны. Их периметры тоже равны.

Площадь квадрата

Запомните!

Для вычисления площади квадрата нужно умножить его длину на саму себя.

S = a · a

Пример:

S_EKFM = EK · EK

S_EKFM = 3 · 3 = 9 см²

Формулу площади квадрата, зная определение степени, можно записать следующим образом:

S = a²

Площадь прямоугольника

Запомните!

Для вычисления площади прямоугольника нужно умножить его длину на ширину.

S = a · b

Пример:

S_ABCD = AB · BC

S_ABCD = 3 · 7 = 21 см²

Запомните!

Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.

Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.

Площадь сложных фигур

Запомните!

Площадь всей фигуры равна сумме площадей её частей.

Задача: найти площадь огородного участка.

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя правило выше.

Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

S_ABCE = AB · BC
S_EFKL = 10 · 3 = 30 м²
S_CDEF = FC · CD
S_CDEF = 7 · 5 = 35 м²

Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = S_ABCE + S_EFKL
S = 30 + 35 = 65 м

2

Ответ: S = 65 м² — площадь огородного участка.

---

Свойство ниже может вам пригодиться при решении задач на площадь.

Запомните!

Диагональ прямоугольника делит прямоугольник на два равных треугольника.

Площадь любого из этих треугольников равна половине площади прямоугольника.

Рассмотрим прямоугольник:

АС — диагональ прямоугольника ABCD. Найдём площадь треугольников ABC и ACD

Вначале найдём площадь прямоугольника по формуле.

S_ABCD = AB · BC
S_ABCD = 5 · 4 = 20 см²

S _ABC = S_ABCD : 2

S _ABC = 20 : 2 = 10 см²

S _ABC = S _ACD = 10 см²

Определение площади Формулы площадей фигур

7 способов найти площадь прямоугольника

10 марта 2020 Ликбез Образование

Выбирайте формулу, ориентируясь на известные величины.

1. Если известны две соседние стороны

Просто перемножьте две стороны прямоугольника.

• S — искомая площадь прямоугольника;
• a и b — соседние стороны.

2. Если известны любая сторона и диагональ

Найдите квадраты диагонали и любой стороны прямоугольника.

От первого числа отнимите второе и найдите корень из результата.

Умножьте длину известной стороны на полученное число.

• S — искомая площадь прямоугольника;
• a — известная сторона;
• d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).

3. Если известны любая сторона и диаметр описанной окружности

Найдите квадраты диаметра и любой стороны прямоугольника.

От первого числа отнимите второе и найдите корень из результата.

Умножьте известную сторону на полученное число.

• S — искомая площадь прямоугольника;
• a — известная сторона;
• D — диаметр описанной окружности.

4. Если известны любая сторона и радиус описанной окружности

Найдите квадрат радиуса и умножьте результат на 4.

Отнимите от полученного числа квадрат известной стороны.

Найдите корень из результата и умножьте на него длину известной стороны.

• S — искомая площадь прямоугольника;
• a — известная сторона;
• R — радиус описанной окружности.

5. Если известны любая сторона и периметр

Умножьте периметр на длину известной стороны.

Найдите квадрат известной стороны и умножьте полученное число на 2.

От первого произведения отнимите второе и разделите результат на 2.

• S — искомая площадь прямоугольника;
• a — известная сторона;
• P — периметр прямоугольника (равен сумме всех сторон).

6. Если известны диагональ и угол между диагоналями

Найдите квадрат диагонали.

Разделите полученное число на 2.

Умножьте результат на синус угла между диагоналями.

• S — искомая площадь прямоугольника;
• d — любая диагональ прямоугольника;
• α — любой угол между диагоналями прямоугольника.

7. Если известны радиус описанной окружности и угол между диагоналями

Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.

Умножьте полученное число на 2, а потом на синус угла между диагоналями.

• S — искомая площадь прямоугольника;
• R — радиус описанной окружности;
• α — любой угол между диагоналями прямоугольника.

Читайте также 🎓❓📐

• ТЕСТ:​ ​​Умеете ли вы считать в уме?
• Как легко и быстро считать проценты в уме
• Как найти площадь любого треугольника
• ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
• Как освоить устный счёт школьникам и взрослым

Как рассчитать площадь | Что?, Вычисления, Единицы, Примеры

Примечание: эта страница содержит устаревшие ресурсы, которые больше не поддерживаются. Вы можете продолжать использовать эти материалы, но мы можем поддерживать только наши текущие рабочие листы, доступные как часть нашего членского предложения.

Что такое площадь?

Площадь сообщает нам размер формы или фигуры. Он сообщает нам размер квадратов, прямоугольников, кругов, треугольников, других многоугольников или любой замкнутой фигуры.

В реальном мире он говорит нам о размере листков бумаги, экранов компьютеров, комнат в домах, бейсбольных полей, городов, городов, стран и так далее. Знание местности может быть очень важным. Подумайте о том, чтобы постелить новый ковер в комнате вашего дома. Зная площадь комнаты, вы сможете убедиться, что ковер, который вы покупаете, достаточно большой, и в нем не останется лишнего.

Вычисление площади

Площадь измеряется в квадратах (или квадратных единицах).

Сколько квадратов в этом прямоугольнике?

Мы можем посчитать квадраты или взять длину и ширину и использовать умножение. Прямоугольник выше имеет площадь 15 квадратных единиц.

Площадь прямоугольника = длина x ширина

Примеры расчета площади прямоугольника

Единицы измерения площади

Мы измеряем площадь квадратами. Мы используем разные размеры квадратов в зависимости от того, насколько велика или мала площадь.

Пример	Длина стороны квадрата	Блок
Размер ногтя на большом пальце	Миллиметр	мм 2
Размер листа бумаги	Сантиметр	см 2
Размер комнаты	Счетчик	м 2
Размер города	км	км 2

Не забудь пи 2

Мы пишем квадратные размеры, используя маленькую 2 рядом с единицей измерения. Пишем мм 2 , см 2 , м 2 , км 2 , см 2 Мы можем сказать «63 квадратных миллиметра» или «63 квадратных миллиметра»

Мы могли бы использовать маленькие квадраты для измерения больших площадей. Единственная проблема заключается в том, что в конечном итоге нам придется использовать очень большие числа. Например, поле может быть измерено в 5 000 000 000 квадратных миллиметров, тогда как 5000 квадратных метров было бы гораздо легче произносить, писать и визуализировать.

Возможно, вы услышите больше единиц измерения площади; квадратные дюймы, квадратные футы, квадратные ярды, квадратные мили, акры, гектары — все это единицы измерения площади.

Дополнительные примеры вычисления площади

Площадь квадрата

Длина и ширина квадрата одинаковы, поэтому нам просто нужно умножить длину на длину.

Площадь круга

Площадь круга = πr ²
, где r — радиус круга, а π — отношение длины окружности к ее диаметру.

π (произносится как «пирог» и часто пишется как «пи») — бесконечное десятичное число с общим приближением 3,14159. Вы можете узнать больше о Пи здесь . Обратите внимание, как по мере того, как сектора становятся меньше, форма становится больше похожей на прямоугольник. Примечание. Нет предела тому, насколько маленькими могут быть эти сектора и насколько близко они могут напоминать прямоугольник при расположении.

Предполагая, что мы знаем, что длина окружности равна 2πr, мы можем добавить размеры к «прямоугольнику», как показано ниже. Используя формулу площади прямоугольника, площадь = ширина x высота, мы можем увидеть, как можно показать, что наш круг, преобразованный в прямоугольник, имеет площадь, которая приблизительно равна 90 150 πr  x  r  или  πr ^{. 2}

Секторы круга переставлены

Секторы круга переставлены – начинают выглядеть как прямоугольник

Площадь составных фигур

Существует много случаев, когда для расчета общей площади требуется вычислить более одной площади, а затем выполнить сложение, вычитание или какую-либо другую комбинацию операций для нахождения требуемой площади.

Примечание: В приведенных ниже примерах единицы измерения не показаны, а ответы и значение π (Пи) округлены до сотых.

Пример: простые составные формы

Приведенный ниже пример расчета площади относительно прост. Форму можно рассматривать как треугольник в сочетании с прямоугольником.

Приведенный выше пример иллюстрирует распространенное требование при работе с составными формами — поиск размеров, которые не показаны. Обучая своих детей, при необходимости помогите найти эти «недостающие» измерения. Ниже приведен еще один пример.

Нахождение размеров

Пример: вычитание одной площади из другой

В приведенном ниже примере фигура выглядит как прямоугольник с вырезанным треугольником.

Пример: Частичные площади

Приведенный ниже пример аналогичен приведенному выше, но, поскольку у нас есть полукруг, нам нужно вычислить часть (половину) площади круга. Обратите внимание, что в этом примере показан диаметр, а не радиус.

Пример: Решения! Объединить? Вычтите

Обычно имеется более одного способа вычисления конечной площади. В приведенных ниже примерах фигура может быть представлена ​​как два объединенных прямоугольника или как один большой прямоугольник с меньшим прямоугольником, «вырезанным» из правого верхнего угла.

Рабочие листы для расчета площади

Распечатайте приведенные ниже рабочие листы и используйте их для практики при обучении ваших детей.

• Вычисление площадей — прямоугольники и квадраты
• Вычисление площадей — прямоугольники
• Вычисление площадей — прямоугольники
• Вычисление составных площадей, например. с прямоугольными формами
• Вычисление составных площадей, например, с прямоугольниками, треугольниками и кругами
• Вычисление площадей, например, треугольников
• Площадь круга
• Расчет площади поверхности, например прямоугольных призм

Здесь вы найдете другие рабочие листы по геометрии для печати.

Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!

Как найти площадь поверхности прямоугольной призмы (формула + видео)

Автор:

Малкольм МакКинси

16 января 2023 г.

Факт проверено

Пол Маццола

Что такое прямоугольник?

Перед тем, как найти площадь прямоугольника, убедитесь, что у вас действительно есть прямоугольник. По определению  90 252 прямоугольник 90 253  является четырехгранной фигурой, все углы которой прямые, равные 90 градусам.

Вы можете распознать прямоугольник, проверив два его идентифицирующих свойства :

Единственный способ построить многоугольник, удовлетворяющий этим двум требованиям, — это сделать прямоугольник. Итак, проверьте, есть ли у вас плоская, замкнутая, четырехгранная форма (это плоская фигура, четырехугольник с внутренней и внешней сторонами). Если все в порядке, посмотрите, есть ли у него четыре внутренних угла, каждый из которых равен 90 252 90° 90 253 с противоположными параллельными конгруэнтными сторонами.

Если ваша фигура обладает всеми этими качествами, у вас есть прямоугольник, и вы можете найти его площадь.

Площадь прямоугольника

Площадь прямоугольника

Площадь — это количество плоского пространства внутри прямоугольника или замкнутой формы. Он всегда выражается в квадратных единицах линейного измерения. Итак, если фигура имеет длину 11 ярдов и ширину 7 ярдов , ее площадь выражается в квадратных ярдах, даже если фигура не квадратная.

Площадь никогда не является линейной мерой.

Квадратная единица чего-либо равна одной единице длины, умноженной на одну единицу ширины. Вот некоторые распространенные линейные измерения, их квадратные единицы, а также способы их написания и сокращения: 9{2}м2

Каждый раз вы просто берете единицу измерения длины и умножаете ее на саму себя (возводите ее в квадрат). Вы делаете это, потому что пытаетесь понять, сколько замкнутого пространства содержит фигура.

Формула площади прямоугольника

Формула для площади прямоугольника:

Если вы не знаете, какова длина прямоугольника, эта формула не принесет вам много пользы. Поэтому убедитесь, что вы можете определить два линейных измерения прямоугольника.

Под длиной любого многоугольника всегда понимается его большее измерение, даже если его длина не представлена ​​по горизонтали.

Как найти площадь прямоугольника

Представьте, что вы устанавливаете в комнате новый ковер от стены до стены. Это очень распространенное использование для определения площади. Комната 4 метра в длину и 3 метра в ширину. Чтобы добраться до всех четырех углов (от стены до стены), ваш ковер также должен быть 4 метра в длину и 3 метра широкий.

Как найти площадь прямоугольника

Уравнение площади прямоугольника

Площадь пола и ковра:

Как найти площадь прямоугольника

Следующий пример является чрезвычайно распространенным практическим применением для нахождения площади прямоугольников.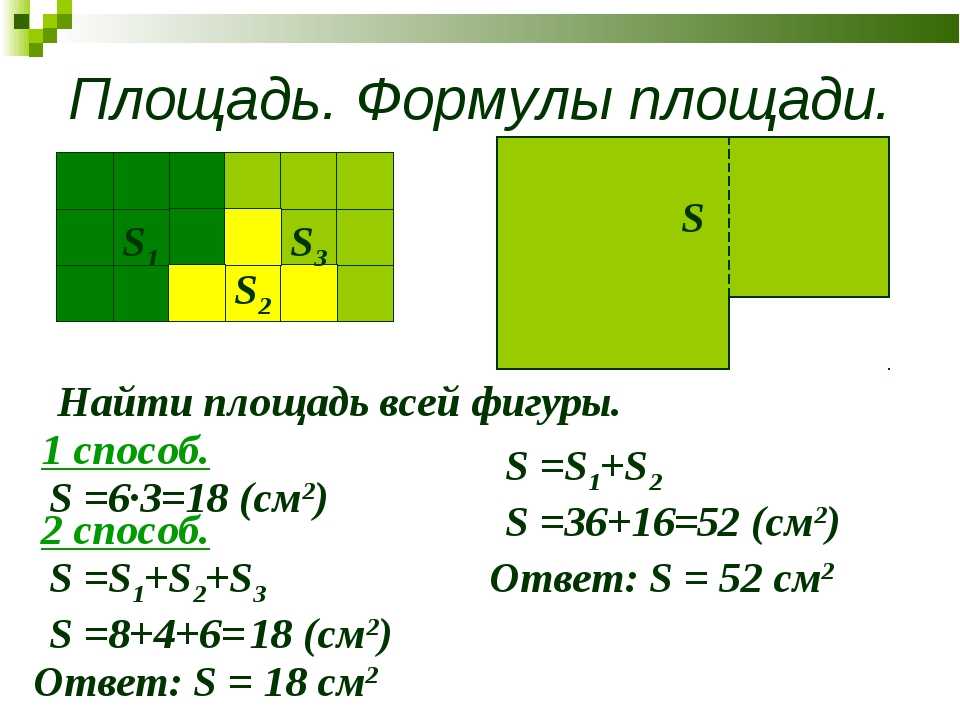 . Предположим, вы перекрашиваете стены своей спальни. Если не учитывать места для окон, дверей шкафа и двери в спальню (краски вы всегда покупаете чуть больше, чем вам понадобится!), вот размеры стен:

• North wall: 8′ tall and 9′ wide

• East wall: 8′ tall and 12′ wide

• South wall: 8′ tall and 9′ ширина

• Западная стена: высота 8 футов и ширина 12 футов

Пример области прямоугольника

Обратите внимание, что все стены имеют одинаковую высоту. Также обратите внимание, что северная и южная стены имеют одинаковую ширину, а восточная и западная стены имеют одинаковую ширину. Вы знаете, что ваша спальня представляет собой прямоугольник. 9{2}96ft2

Вы можете быстро добавить их, чтобы узнать, что вашей комнате требуется 336 квадратных футов покрытия краской. Типичный галлон краски покрывает 400 квадратных футов , поэтому вам понадобится один галлон краски.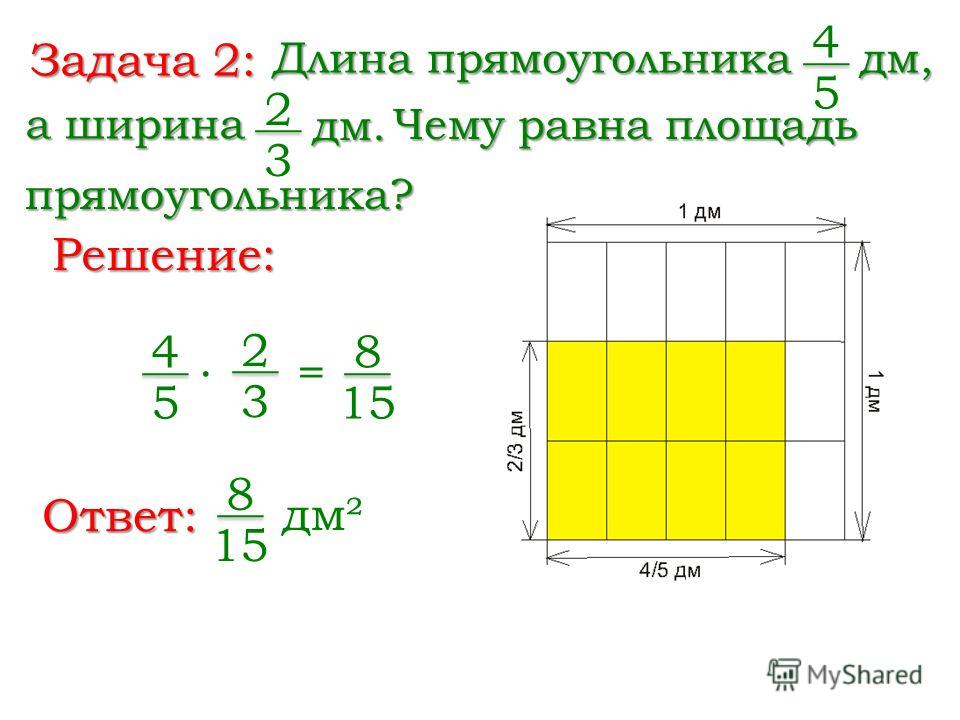

Как вычислить площадь прямоугольника

Предположим, вам нужно мягкое одеяло для дневной конуры вашей собаки. Пол конуры имеет размеры 54 дюйма длины и 36 дюймов ширины. Какая площадь одеяла вам нужна?

Вычислите площадь прямоугольника

Площадь прямоугольника examples

Допустим, вам нужен новый приветственный коврик перед входной дверью вашего дома. Вы видите один размером 75 сантиметров (см) в длину и 40 см в ширину. Какова площадь дверного коврика?

Площадь прямоугольника пример задачи 2

Пример #3

Площадь часто связана с ценообразованием. Ковер продается в квадратных ярдах или квадратных метрах. Напольная плитка продается квадратными метрами. Даже такие вещи, как строительство новых зданий и аренда недвижимости, рассчитываются как затраты на квадратный фут или квадратный метр.

Знание того, как найти площадь прямоугольника, поможет вам найти выгодные предложения и избежать траты денег.